本文为2016年bctf中的LostFlower的writeup。

1

LostFlower writeup

首先点我下载题目，直接使用jeb反编译，入口代码如下：
2
可以看到，Java逻辑十分简单，首先获取用户输入，然后调用Double.parseDouble将其转为Double类型（这意味着输入数据必须为合法的Double数据），接着将其作为参数传递给native层的stringFromJNI，如果返回值为6，则调用stringFromJNI2，其返回值即为Flag。
使用IDA反汇编，结果如下：
3
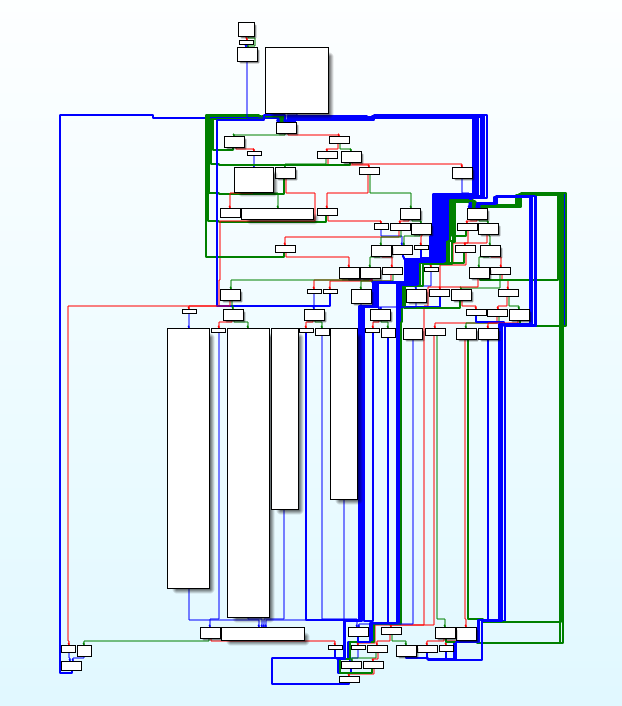
可以看到，SO进行了高强度的混淆，加入了大量的while、if等无用指令。
对stringFromJNI使用f5，奇怪的是，经过对f5伪代码的分析，并没有发现有对用户输入进行校验的地方，难道是程序做了处理，导致f5出现了错误？静态分析解决不了，我们就用动态调试。SO没有做任何反调试处理，而且发现动态调试时，stringFromJNI的f5可以得到正确的伪代码。
由于汇编代码含有大量的无效跳转，因此我们选择直接在伪代码的基础上进行动态调试，经过几轮动态调试，发现stringFromJNI包含3处关键代码（即有对输入数据进行判断或处理的地方），如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
...
// 第68行
  v59 = a4; // a4为输入值的小数部分
  v58 = a3; // a3为输入值的整数部分
  v67 = _stack_chk_guard;
  v60 = j_j___aeabi_d2iz(a3, a4);   // v60为输入值的整数部分
...
// 第112行
else if ( (signed int)v6 > 814185195 )
{
if ( v6 == (void *)814185196 )
{
  v6 = &unk_60130C76;
  if ( v65 <= 1000000000 )  // v65为输入值的整数部分
    v6 = (void *)306644219;
}
}
···
// 第398行
  v13 = check1(*v62);   // *v62为输入值的整数部分
  v14 = 1;
  if ( !v13 )
    v14 = 0;
  v63 = v14;
  v4 = (const char *)-439993678;
}
else if ( v4 == (const char *)-439993678 )
{
  v9 = (unsigned __int8)v63;
  v4 = (const char *)&unk_662944DE;
  goto LABEL_49;
}
...

从上面的代码我们可以得出以下3点结论：

  1. stringFromJNI只对输入Double数据的整数部分做处理。
  2. stringFromJNI将整数部分和1000000000做比较，根据大小不同，进入不同的分支。
  3. stringFromJNI调用了check1，参数为整数部分，根据返回值是否为1，进入不同的分支。

现在我们开始脑洞一番，一般情况下，我们测试的时候，不会输入一个大于1000000000的数据，基于这一点我们猜测输入数据应大于1000000000；程序员的逻辑中，返回1是真，0是假，因此我们猜测check1的返回应为1。现在我们测试一番，首先在check1的后面一行下断点，接着输入一个大于1000000000的数据，如1000000001，点击提交按钮，程序断下来以后，可以看到r0为0，修改r0为1，最后让程序继续运行，可以发现，程序成功打印出了Flag，然而由于我们是直接修改的返回值，而输入依然是错误的，自然这个Flag也是错误的。不过，可以确定的是我们的猜测是正确的，即输入数据应大于1000000000并且check1的返回值为1。因此现在的关键即为分析check1，同样在动态分析时，对check1进行f5得到伪代码，check1的逻辑要更加简单一点，我们可以直接采用逆推的方法，也就是从出口（return）开始，往函数入口方向逆向推理的过程。逆推过程这里不再详述，只需要注意以下3点即可加快效率：

  1. 不要在意大于或小于的比较，我们只需要关注等于时的分支。
  2. 在IDA里，你可以选择一个值，此时所有这个值都会标黄，从而可以快速找到下一个值。
  3. 我们可以直接在IDA f5伪代码里下断点，也就是说可以直接以伪代码级别调试。

给出逆推的结果，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
...
// 第134行
if ( v2 == (void *)-427046904 )
{
LABEL_15:
    v2 = (void *)196778168;
    LOBYTE(v1) = 1; // 2）就是这里，v1赋值为1了，也就是说我们要找到v2 = -427046904的地方。
}
...
                    }
                    if ( (signed int)v2 > -109345567 )
                      break;
                    if ( v2 == (void *)-242797719 )
                      goto LABEL_28;
                  }
                  if ( (signed int)v2 > -32671955 )
                    break;
                  if ( v2 == (void *)-109345566 )
                  {
                    sub_7509FAA4(v17 - 631823485 - v18 + 631823485);
LABEL_28:
                    v2 = (void *)56101389;
                  }
                }
                if ( (signed int)v2 > 32634615 )
                  break;
                if ( v2 == (void *)-32671954 )
                {
                  v5 = j_j___aeabi_i2d(v3);
                  v7 = j_j_pow_0(0, 1076101120, v5, v6);
                  v9 = j_j___aeabi_d2iz(v7, v8);
                  v10 = j_j___aeabi_idiv(v17, v9);
                  v11 = j_j___modsi3(v10, 10);
                  v12 = my_pow(v11);
                  v18 = -(-v18 - v12);
                  v2 = (void *)142850058;
                }
              }
              if ( (signed int)v2 > 56101388 )
                break;
...
// 第171行
if ( v2 == (void *)32634616 )   // 3）找到v2 = 32634616的地方。
{
    v2 = (void *)-427046904;
    v4 = -1611885754;
    if ( !v29 ) // v29要为1，不然就跳到LABEL_35去了，LABEL_35会改变v2的值。
        goto LABEL_35;
}
...
// 第181行
if ( v2 == (void *)56101389 )   // 4）找到v2 = 56101389的地方，事实上不用在往前找了，这里就是判断的地方。
{
    v13 = sub_7509FAA4((char *)&unk_59357062 + v17 - v18 - 0x59357062);
    v14 = 1;
    if ( v13 >= 0 ) // v13需要小于0
        v14 = 0;
    v29 = v14;  // 因为v29为1，因此v14要为1。
    v2 = (void *)32634616;
}
...
// 第212行
  return v1;    // 1）这里是返回，也就是逆推入口，我们要找到对r1赋值为1的地方。
...

从上面注释可以知道，也就是需要sub_7509FAA4((char *)&unk_59357062 + v17 - v18 - 0x59357062);返回负数，现在我们需要做的就是搞清v17和v18的值是什么，以及sub_7509FAA4的逻辑。关键代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
...
// 第33行
v17 = a1;   // a1为整数部分，也就是v17也为整数部分
...
// 第73行
if ( v2 == &unk_4A2AC114 )
{
    v2 = (void *)-32671954;
    v4 = -242797719;
    if ( v3 >= 10 ) // 这里是一个for循环的跳出条件
LABEL_35:
        v2 = (void *)v4;
}
...
// 第126行
if ( v2 == (void *)-1521320686 )
{
    ++v3;   // for循环里的自增
    v2 = (void *)-1898177542;
}
...  
// 第157行
if ( v2 == (void *)-32671954 )  // 这里面是for循环的主体
{
    v5 = j_j___aeabi_i2d(v3);
    v7 = j_j_pow_0(0, 1076101120, v5, v6);
    v9 = j_j___aeabi_d2iz(v7, v8);
    v10 = j_j___aeabi_idiv(v17, v9);
    v11 = j_j___modsi3(v10, 10);
    v12 = my_pow(v11);
    v18 = -(-v18 - v12);
    v2 = (void *)142850058;
}
...

v17为用户输入的Double数据的整数部分，v18在for循环里完成了赋值，那么这个for循环到底干了什么？我们先看前面几行代码：

1
2
3
4
5
v5 = j_j___aeabi_i2d(v3);
v7 = j_j_pow_0(0, 1076101120, v5, v6);
v9 = j_j___aeabi_d2iz(v7, v8);
v10 = j_j___aeabi_idiv(v17, v9);
v11 = j_j___modsi3(v10, 10);

这里几个函数都是一些除法、求余的操作。经过几轮动态调试，事实上，这个for循环的前五行代码就是逆向取出一个10位整数的每一位。举个例子，输入为1234567890，每一轮得到的依次为0，9，8，7，6，5，4，3，2，1。
现在还剩下一个my_pow,顾名思义这是个幂相关的函数。注意我们不需要去具体分析my_pow,因为我们的输入只有0-9这10种可能，几轮测试过后，得到结论：my_pow返回输入数据的十次幂。
用C代码重现下这个for循环：

1
2
3
4
5
6
7
8
9
10
11
int i;
int integer; // 用户输入的整数部分
int out;    // 即v12
out = 0;
for (i = 0; i < 10; ++i) {
    int x;
    
    x = integer / pow(10, i) % 10;
    out += pwo(x, 10);
}

ok，现在sub_7509FAA4((char *)&unk_59357062 + v17 - v18 - 0x59357062);中，我们知道v17为用户输入数据的整数部分，v18为上面的out，剩下的是分析sub_7509FAA4的功能，f5得到伪代码，代码很短，而且逻辑也很简单，逻辑是这样的：如果参数（v17 - v18）为非负数直接返回该参数，如果参数为负数则求补之后返回。
这里遇到一个问题，由上面分析可知，需要sub_7509FAA4返回负数，但是按照该函数逻辑，无论如何都会返回一个非负数！什么情况？经过1个小时的重新分析，排除了前面分析错误的情况，那么sub_7509FAA4存在溢出？这个时候看伪代码已经没用了，通过对sub_7509FAA4的汇编代码的分析，发现了溢出点：NEGS R1, R1，当参数为负数时，程序使用NEGS指令求补后返回，其中NEGS的作用是这样的：将目的操作数的所有数据位取反加1。当参数为0x80000000（这是个负数）时，所有数据位取反后为0x8fffffff，再加1后发生溢出，最后值为0x80000000。也就是说，0x80000000经过NEGS后仍然为0x80000000。
终上所述，现在给出结论：

  1. 输入数据为一个合法的十位Double数据，设其整数部分为integer。
  2. 对integer的每一位求10次幂，并全部加起来，结果为sum。
  3. integer -sum == 0x80000000。

最后给出计算输入的程序：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
int main()
{
	int pow_table[] = {0, 1, 0x400, 0xe6a9, 0x100000, 0x9502f9, 0x39aa400, 0x10d63af1, 0x40000000, 0xcfd41b91};
	int i;
	for (i = 1000000000; i <= 0x80000000; ++i) {
		int a0 = i % 10;
		int a1 = (i % 100) / 10;
		int a2 = (i % 1000) / 100;
		int a3 = (i % 10000) / 1000;
		int a4 = (i % 100000) / 10000;
		int a5 = (i % 1000000) / 100000;
		int a6 = (i % 10000000) / 1000000;
		int a7 = (i % 100000000) / 10000000;
		int a8 = (i % 1000000000) / 100000000;
		int a9 = i / 1000000000;
		
		int sum = pow_table[a0] + pow_table[a1] + pow_table[a2] + pow_table[a3] + pow_table[a4] + pow_table[a5] + pow_table[a6] + pow_table[a7] + pow_table[a8] + pow_table[a9];
		if (((i - sum) & 0xffffffff) == 0x80000000) 
		{
			printf("ok, %d\n", i);
			break;
		}
		if(i % 1000000 == 0)
		{
			printf("%d\n",i);
		}
	}
	return 0;
}

程序跑一会就出来了，输入为1422445956，最后的Flag为：BCTF{wrhav3f4nwxo}。